Thuật toán K láng giềng gần nhất (K-Nearest Neighbor - KNN) là gì?
Mục Lục
Thuật toán K láng giềng gần nhất (K-Nearest Neighbor - KNN)
Thuật toán K láng giềng gần nhất trong tiếng Anh là K-Nearest Neighbor, viết tắt là KNN.
Thuật toán K láng giềng gần nhất là một kĩ thuật học có giám sát (supervised learning) dùng để phân loại quan sát mới bằng cách tìm điểm tương đồng giữa quan sát mới này với dữ liệu sẵn có.
Ví dụ
Ví dụ 1:
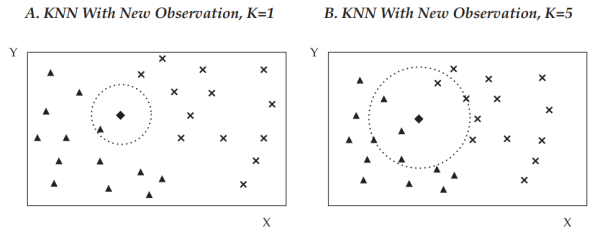
Hình 1
Hình thoi trong Hình 1 đang cần được phân loại thuộc hình chữ thập hoặc hình tam giác.
- Nếu k = 1, hình thoi sẽ được phân loại vào cùng loại với điểm dữ liệu gần nhất của nó (tức là hình tam giác trong bảng bên trái - bảng A).
- Bảng bên phải (bảng B) thể hiện trường hợp k = 5, thuật toán sẽ xem xét 5 điểm dữ liệu gần hình thoi nhất, đó là 3 hình tam giác và 2 hình chữ thập. Qui tắc quyết định là chọn phân loại có số lượng lớn nhất trong 5 điểm dữ liệu được xem xét. Vì vậy, trong trường hợp này, hình thoi cũng được xếp vào phân loại tam giác.
Ví dụ 2:
Giả sử chúng ta có một cơ sở dữ liệu về trái phiếu doanh nghiệp được phân loại theo xếp hạng tín dụng.
Cơ sở dữ liệu này chứa thông tin chi tiết về các đặc điểm của các trái phiếu:
- Đặc điểm của công ty phát hành: qui mô tài sản, ngành, tỉ lệ đòn bẩy, tỉ lệ dòng tiền)
- Đặc điểm của trái phiếu: kì hạn, lãi suất cố định/thả nổi, quyền chọn đính kèm)
Một trái phiếu sắp được phát hành mà không có xếp hạng tín dụng. Về bản chất, trái phiếu doanh nghiệp có đặc điểm tương tự sẽ được xếp hạng tín dụng tương tự. Vì vậy, bằng cách sử dụng KNN, chúng ta có thể dự đoán xếp hạng tín dụng của trái phiếu mới dựa trên sự tương đồng về đặc điểm của nó với trái phiếu trong cơ sở dữ liệu của chúng ta.
Ứng dụng
KNN là một mô hình đơn giản và trực quan nhưng vẫn có hiệu quả cao vì nó không tham số; mô hình không đưa ra giả định nào về việc phân phối dữ liệu. Hơn nữa, nó có thể được sử dụng trực tiếp để phân loại đa lớp.
Thuật toán KNN có nhiều ứng dụng trong ngành đầu tư, bao gồm dự đoán phá sản, dự đoán giá cổ phiếu, phân bổ xếp hạng tín dụng trái phiếu doanh nghiệp, tạo ra chỉ số vốn và trái phiếu tùy chỉnh.
Lưu ý khi sử dụng thuật toán KNN
- Một thách thức quan trọng của KNN là xác định thước đo để tính khoảng cách giữa đối tượng cần phân lớp với các đối tượng còn lại trong cơ sở dữ liệu. Vì đây là lựa chọn mang tính chủ quan nên nếu chọn thước đo không phù hợp thì mô hình sẽ không hiệu quả.
Ví dụ, nếu một nhà phân tích đang xem xét sự tương đồng về hiệu suất của các cổ phiếu khác nhau trên thị trường, anh ta có thể xem xét sử dụng mối tương quan của lợi nhuận trong quá khứ giữa các cổ phiếu như một thước đo.
- Kiến thức về dữ liệu và hiểu biết về các mục tiêu của phân tích là các bước quan trọng trong quá trình xác định đặc điểm tương đồng.
Kết quả KNN có thể nhạy cảm với việc bao gồm các đặc điểm không liên quan hoặc tương quan, do đó cần phải chọn các đặc điểm một cách thủ công. Bằng cách đó, nhà phân tích loại bỏ thông tin ít giá trị hơn để giữ thông tin liên quan và phù hợp nhất.
Nếu được thực hiện chính xác, quá trình này sẽ tạo ra một thước đo khoảng cách điển hình hơn. Các thuật toán KNN có xu hướng hoạt động tốt hơn với một số lượng nhỏ các tính năng.
- Số k là siêu tham số của mô hình (hyperparameter), các giá trị khác nhau của k có thể dẫn đến các kết luận khác nhau. Ví dụ, để dự đoán xếp hạng tín dụng của trái phiếu chưa được xếp hạng, k nên là 3, 15 hay 50 trái phiếu tương tự nhất với trái phiếu chưa được xếp hạng?
Nếu k là số chẵn, có thể không có phân loại rõ ràng. Chọn giá trị cho k quá nhỏ sẽ dẫn đến tỉ lệ lỗi cao và độ nhạy đối với các điểm dữ liệu bất thường mang tính cục bộ. Nhưng chọn giá trị cho k quá lớn sẽ làm giảm đi tính chất khái niệm láng giềng gần nhất vì lấy trung bình quá nhiều kết quả.
Trên thực tế, một số kĩ thuật khác nhau có thể được sử dụng để xác định giá trị tối ưu cho k, cần chú ý đến số lượng các loại (categories) và phân vùng của chúng trong mô hình.
(Tài liệu tham khảo: CFA level II, 2020, Quantitative methods)

