Nối đồng xu (Matching Pennies) trong kinh tế học hành vi là gì? Cách thực hiện trò chơi nối đồng xu
Mục Lục
Nối đồng xu (Matching Pennies)
Nối đồng xu trong tiếng Anh là Matching Pennies.
Nối đồng xu là một ví dụ về lí thuyết trò chơi cơ bản giải thích việc làm thế nào những người ra quyết định hợp lí tìm cách tối đa hóa phần thưởng của họ. Nối đồng xu đề cập đến hai người chơi đồng thời đặt một đồng xu trên bàn, với mức chi trả tùy thuộc vào việc hai đồng xu này có khớp nhau hay không.
Nếu cả hai đồng xu đều là mặt ngửa hoặc mặt sấp, người chơi đầu tiên sẽ thắng và giữ đồng xu của người kia; nếu chúng không khớp, người chơi thứ hai sẽ thắng và giữ đồng xu của người kia. Nối đồng xu là một trò chơi có tổng bằng 0, trong đó người chơi này thắng thì người sẽ thua.
Vì mỗi người chơi có xác suất chọn mặt ngửa hoặc mặt sấp bằng nhau và lựa chọn một cách ngẫu nhiên, không có cân bằng Nash trong tình huống này; nói cách khác, không người chơi nào có động lực để thực hiện một chiến lược khác.
Cách thực hiện trò chơi nối đồng xu
Nối đồng xu về mặt khái niệm nó tương tự như trò chơi "Búa, Bao, Kéo" hay trò chơi "lẻ và chẵn".
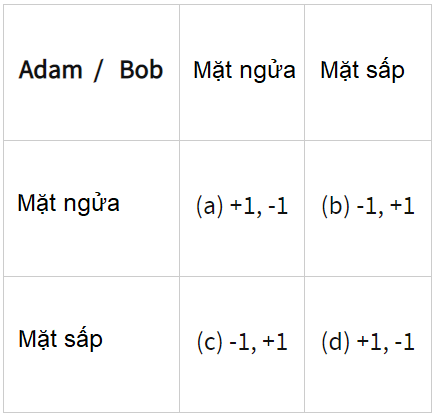
Hãy xem xét ví dụ sau. Adam và Bob là hai người chơi trong trường hợp này và bảng dưới đây cho thấy ma trận tiền thưởng của họ. Trong bốn bộ số được hiển thị trong các ô được đánh dấu từ (a) đến (d), chữ số đầu tiên đại diện cho phần thưởng của Adam, trong khi mục thứ hai đại diện cho phần thưởng của Bob. +1 có nghĩa là người chơi giành được 1 xu, trong khi -1 có nghĩa là người chơi mất 1 xu.
Nếu cả Adam và Bob đều ra "mặt ngửa", thì tiền thưởng được thể hiện như trong ô (a). Nếu Adam chơi "mặt ngửa" còn Bob chơi "mặt sấp", thì tiền thưởng bị đảo ngược, được hiển thị trong ô (b), bây giờ sẽ là -1, +1, có nghĩa là Adam mất 1 xu và Bob kiếm được 1 xu.
Tương tự như vậy, nếu Adam ra "mặt sấp" và Bob ra "mặt ngửa" thì tiền thưởng thể hiện trong ô (c) là -1, +1. Nếu cả hai đều ra "mặt sấp" thì tiền thưởng được thể hiện trong ô (d) là +1, -1.
Tiền thưởng không đối xứng
Trò chơi tương tự cũng có thể được thực hiện với số tiền thưởng cho mỗi người chơi không giống nhau. Thay đổi số tiền thưởng cũng thay đổi chiến lược tối ưu cho người chơi. Ví dụ: nếu mỗi lần cả hai người chơi chọn "mặt ngửa" thì Adam đều nhận được 5 xu thay vì 1 xu thì Adam có mức phần thưởng dự kiến lớn hơn là khi chơi "mặt ngửa" với "mặt sấp".
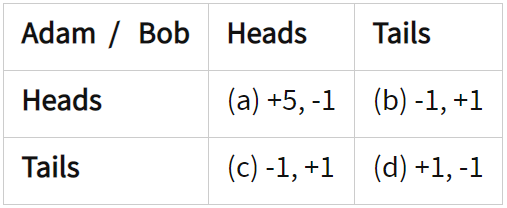
Để tối đa hóa phần thưởng dự kiến của mình, giờ đây Bob sẽ chọn thêm "mặt sấp". Bởi vì đây là một trò chơi có tổng bằng 0, trong đó chiến thắng của Adam lại là mất mát của Bob nên bằng lựa chọn "mặt sấp" của Bob nó bù đắp lại cho phần thưởng nhiều hơn của Adam. Adam sẽ tiếp tục chơi "mặt ngửa" vì phần tiền thưởng nhiều hơn của anh ấy từ việc nối "mặt ngửa" hiện đang được bù đắp bởi khả năng lớn là Bob sẽ chọn "mặt sấp".
(Tài liệu tham khảo: investopedia.com)

