Dòng tiền đều vô hạn (Perpetuity) là gì? Công thức tính dòng tiền đều vô hạn
Mục Lục
Dòng tiền đều vô hạn
Khái niệm
Dòng tiền đều vô hạn hay dòng niên kim vĩnh cửu trong tiếng Anh là Perpetuity.
Trong tài chính, dòng tiền đều vô hạn là một dòng tiền liên tục có giá trị bằng nhau và không có điểm kết thúc. Công thức để tính giá trị hiện tại của dòng tiền đều vô hạn hoặc chứng khoán với dòng tiền dòng tiền đều vô hạn là:
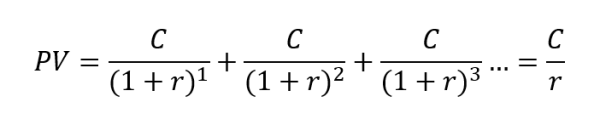
Hình minh họa.
Trong đó:
- C là dòng tiền đều hằng năm.
- r là tỉ lệ lãi suất chiết khấu.
Khái niệm dòng tiền đều vô hạn được sử dụng trong một số lí thuyết tài chính như trong mô hình chiết khấu cổ tức (DDM).
Chứng khoán trả dòng tiền đều vô hạn được gọi là trái phiếu vĩnh viễn hay trái phiếu không có thời hạn.
Đặc điểm
Dòng tiền đều vô hạn là một dòng tiền, một loại niên kim tồn tại mãi mãi tạo thành dòng tiền không có điểm kết thúc.
Trong tài chính, phép tính dòng tiền đều vô hạn được sử dụng trong các phương pháp định giá để tìm ra giá trị hiện tại của dòng tiền một công ty bằng cách chiết khấu bởi một mức tỉ lệ nhất định.
Một ví dụ điển hình về công cụ tài chính có dòng tiền đều vô hạn là trái phiếu do chính phủ Anh phát hành được gọi là consol. Bằng cách mua một consol từ chính phủ Anh, trái chủ có quyền nhận được khoản thanh toán lãi hàng năm kéo dài cho đến mãi mãi.
Tuy có vẻ hơi phi logic, một số dòng tiền đều vô hạn có giá trị hiện tại hữu hạn do tính chất giá trị thời gian của tiền, mỗi khoản thanh toán trong dòng tiền chỉ là một phần rất nhỏ của giá trị cuối cùng. Cụ thể, công thức dòng tiền đều vô hạn sẽ xác định dòng tiền trong năm hoạt động cuối cùng.
Trong định giá tài sản, một công ty được cho là một giá trị hoạt động (going concern) có nghĩa là nó sẽ tiếp tục họat động mãi mãi. Vì lí do này, năm hoạt động cuối cùng là vô hạn nên các nhà phân tích sử dụng công thức dòng tiền đều vô hạn để tìm giá trị của công ty này.
Công thức tính dòng tiền đều vô hạn
Phương pháp nền tảng được sử dụng để tính toán dòng tiền đều vô hạn là chia dòng tiền cho một mức tỉ lệ chiết khấu. Công thức này được sử dụng để tính giá trị cuối cùng trong dòng tiền cho các mục đích định giá phức tạp.
Nếu dòng tiền tăng trưởng, giá trị cuối cùng của dòng tiền đều vô hạn sẽ bằng ước tính của dòng tiền vào năm thứ n của công ty, nhân với một cộng với tốc độ tăng trưởng dài hạn của công ty, sau đó chia cho chênh lệch giữa chi phí vốn và tốc độ tăng trưởng.
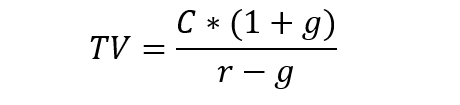
Hình minh họa.
Trong đó:
- TV là giá trị cuối cùng của dòng tiền đều vô hạn.
- r là tỉ lệ lãi suất chiết khấu.
- g là tỉ lệ tăng trưởng của dòng tiền.
Công thức đơn giản hóa tính giá trị hiện tại của giá trị cuối cùng của dòng tiền đều vô hạn bằng dòng tiền cuối cùng chia cho mức tỉ lệ lãi suất chiết khấu trừ đi tỉ lệ tăng trưởng.
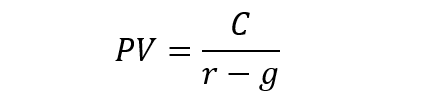
Hình minh họa.
Ví dụ về dòng tiền đều vô hạn
Một công ty dự kiến kiếm được 100,000$ vào năm thứ 10 và chi phí vốn của công ty là 8%, với tốc độ tăng trưởng dài hạn là 3%, giá trị dòng tiền đều vô hạn là:
FV10 = CF10 * (1 + g) / (r – g) = 100,000$ × 1.03 / (0.08 – 0.03) = 2,06 triệu đô la.
Hay có nghĩa là dòng tiền đều vô hạn trả 100.000$ với tỉ lệ tăng trưởng 3% và chi phí vốn 8% có trị giá 2,06 triệu đô la trong vòng 10 năm nữa.
Để đưa giá trị 2.06 triệu đô la về thời điểm hiện tại sử dụng công thức giá trị hiện tại (PV) ở trên.
(Theo Investopedia)

