Biểu đồ hộp (Box Plot) là gì? Đặc trưng và ví dụ
Mục Lục
Biểu đồ hộp (Box Plot)
Biểu đồ hộp trong tiếng Anh là Box Plot hay Box and Whisker plot.
Biểu đồ hộp do John Tukey sáng tạo ra năm 1977.
Biểu đồ hộp (Box plot) hay còn gọi là biểu đồ hộp và râu (Box and whisker plot) là biểu đồ diễn tả 5 vị trí phân bố của dữ liệu, đó là: giá trị nhỏ nhất (min), tứ phân vị thứ nhất (Q1), trung vị (median), tứ phân vị thứ 3 (Q3) và giá trị lớn nhất (max).
Đặc trưng của biểu đồ hộp
- Biểu đồ hộp giúp biểu diễn các đại lượng quan trọng của dãy số như giá trị nhỏ nhất (min), giá trị lớn nhất (max), tứ phân vị (quartile), khoảng biến thiên tứ phân vị (Interquartile Range) một cách trực quan, dễ hiểu.
- Trên biểu đồ hộp, ngoài các đại lượng số trung bình, trung vị, còn thể hiện một số thông số sau:
(1) Số phân tử hay còn gọi là tứ phân vị (Quartiles): Tứ phân vị là đại lượng mô tả sự phân bố và sự phân tán của tập dữ liệu. Số phân tử có 3 giá trị, đó là số phân tử thứ nhất (Q1), thứ nhì (Q2) và thứ ba (Q3). Ba giá trị này chia một tập hợp dữ liệu (đã sắp xếp dữ liệu theo trật từ bé đến lớn) thành 4 phần có số lượng quan sát đều nhau.
Tứ phân vị được xác định như sau:
+ Sắp xếp các số theo thứ tự tăng dần
+ Cắt dãy số thành 4 phần bằng nhau
+ Tứ phân vị là các giá trị tại vị trí cắt

(2) Khoảng biến thiên số phân tử (Interquartile Range - IQR) IQR được xác định như sau:

Ví dụ
Xét một ví dụ về việc sử dụng biểu đồ hộp:
Dưới đây mô tả sử dụng biểu đồ hộp để phân tích, nhận biết vấn đề.
Ví dụ, với số liệu thu thập được về tỉ lệ làm lại (Rework Ratio) trong quá trình sản xuất, (có xmin = 0,0; Q1 = 14,9; x = 19,0; x = 15,8; Q3 = 20,6; xmax =23,2) ta có biểu đồ hộp với hình dáng biểu đồ như sau:
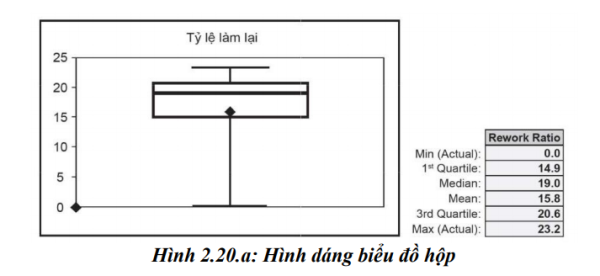
Nguồn: 6 Sigma - Nội dung cơ bản và hướng dẫn áp dụng, NXB Hồng Đức
Trung bình tỉ lệ làm lại là 15,8%, trung vị là 19%.
Dữ liệu có xu hướng nghiêng nhiều về phía trên giá trị trung bình.
Khoảng số phân tử = Q3 - Q1 = 20,6 - 14,9 = 5,7
Khoảng cách giữa giá trị lớn nhất và nhỏ nhất là 23,2 - 0 = 23,2.
Nhìn chung, tỉ lệ làm lại cao và quá trình có sự dao động lớn, không ổn định, kiểm soát chất lượng kém. Tuy nhiên, biểu đồ hộp giúp nhìn trực quan hơn khi so sánh 3 giai đoạn hoặc khu vực khác nhau như hình dưới đây:
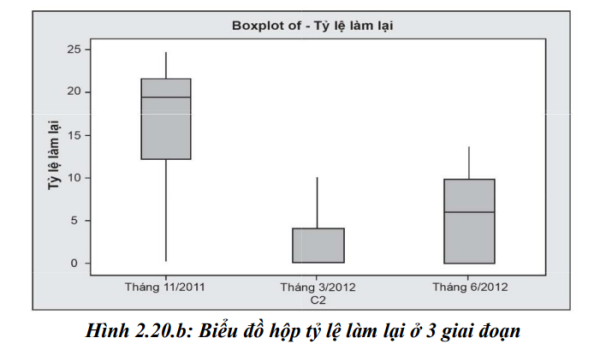
Nguồn: 6 Sigma - Nội dung cơ bản và hướng dẫn áp dụng, NXB Hồng Đức
Nhận xét:
Với ba lần thu thập dữ liệu về tỉ lệ làm lại vào thời điểm tháng 11/2011, tháng 3/2012 và tháng 6/2012, dữ liệu vào thời điểm tháng 11/2011 cho thấy quá trình kiểm soát lỗi kém vì xu hướng tập trung của dữ liệu (trung vị) ở mức cao, độ dao động lớn.
Kiểm soát chất lượng vào thời điểm tháng 3/2012 là tốt nhất vì dữ liệu về tỉ lệ làm lại tập trung ở mức thấp, dao động ở phạm vi hẹp.
(Tài liệu tham khảo: 6 Sigma - Nội dung cơ bản và hướng dẫn áp dụng, NXB Hồng Đức; Box plot review, Khan Academy)

